杨辉三角,是一种像三角形一样的几何排列。在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲,帕斯卡(1623----1662)在1654年发现这一规律,所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年,比贾宪迟600年。
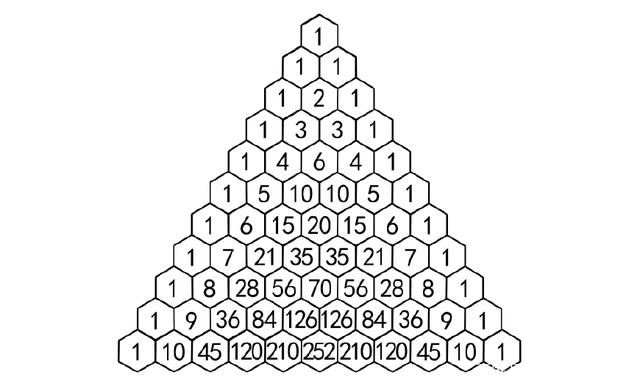
[代码运行结果]
[代码]
# 算法一: 递归
def pasica(n):
'''n 代表三角的层号,从0开始'''
if n==0:
return (1,)
else:
res = (1,)
for i in range(n-1):
res = ( pasica(n-1)[i] pasica(n-1)[i 1] ,)
res = (1,)
return res
# test code
# print( pasica(0) )
# print( pasica(1) )
# print( pasica(2) )
# print( pasica(3) )
# print( pasica(4) )
# print( pasica(5) )
# print( pasica(6) )
# print( pasica(7) )
# print( pasica(8) ) # 开始卡
# print( pasica(9) ) # 很慢了
# 算法二: 用闭包设计缓存机制
def pasica():
'''n 代表三角的层号,从0开始'''
alldata = [(1,),(1,1)] # 设计缓存
def pas(n):
lastestid = len(alldata)-1
if n<=lastestid:
return alldata[n] # 由缓存提取数据
else:
for i in range(n - lastestid ): # 需要在alldata里补充 n - lastestid
tu=[]
lastline = list(alldata[lastestid])
lastline = [0] lastline [0]
# print(lastline,'='*10)
for j, d in enumerate(lastline):
if j 1
tu.append(d lastline[j 1])
alldata.append(tuple(tu))
lastestid = len(alldata)-1
return alldata[n]
return pas
fpas = pasica()
# test
# print( fpas(0) )
# print( fpas(1) )
# print( fpas(2) )
# print( fpas(3) )
# print( fpas(4) )
# print( fpas(5) )
# print( fpas(6) )
# print( fpas(7) )
# print( fpas(8) )
# print( fpas(9) )
def seeoutput( n ):
aa = fpas(n)
weight = len( str( max(aa))) 1
nline = " ".join( [ "{:<{w}}".format(e, w=weight) for e in aa] )
alldata = []
for i in range(n 1):
aa = fpas(i)
iline = " ".join( [ "{:<{w}}".format(e, w=weight) for e in aa] )
print( "{:^{w}}".format(iline, w=len(nline)) )
seeoutput(10)
print()

以上就是关于python编程教程:python的杨辉三角的分享,希望能对你有所帮助。








